Berikut ini soal matematika kelas 9 semester 1 soal Penilaian Akhir Semester (PAS) SMP/MTs kurikulum 2013 Lengkap dengan jawabannya. Pada
artikel ini saya membahas kunci jawaban sebagai bahan latihan sobat mempersiapkan PAS matematika kelas 9 semester gasal.
Dalam pembahasan soal matematika kelas 9 ini dikupas tuntas 30 soal pilihan ganda dan 5 soal esai. Silahkan sobat simak secara seksama
sampai selesai.
Pembahasan soal matematika ini saya rancang agar sobat tidak hanya membaca soal dan jawaban saja, tetapi berupa soal
yang dilampirkan pembahasan kunci jawabannya. Apabila sobat telah mengerjakan dan hendak mengecek benar atau tidak hasil
pengerjaannya, bisa sobat lihat dengan melihat pembahasan.
Dengan begitu kalian bisa membandingkan hasil mengerjakan soal sendiri dengan kunci jawaban yang benar. Jika kalian
tidak bisa mengerjakan sama sekali, sobat juga bisa langsung melihat pembahasan yang telah saya kerjakan.
Pengen tau tips jago matematika ? simak artikel saya pada series Cara Pintar Matematika Tanpa Bimbel. Pada artikel
tersebut saya membongkar tips jago matematika yang pernah dilakukan.
Soal PAS Matematika SMP/MTs Kelas 9
Soal No 1
Hasil dari $\frac{1}{27} \times (3^2)^3$ adalah ...
A. $3$
B. $3^2$
C. $3^3$
D. $3^4$
Mari kita ubah $27$ ke bentuk $(3^3)$ dan bentuk perpangkatan $(3^2)^3$ diubah menjadi $(3^3)^2$.
Sehingga soal di atas bisa ditulis ulang seperti berikut ini
$\frac{1}{27} \times (3^2)^3$
$\frac{1}{3^3} \times (3^3)^2$
$\frac{1}{3^3} \times (3^3) \times (3^3) = 3^3$
Jadi jawaban yang tepat C
Soal No 2
Bila $\frac{9^x \times 3^7 \times 27^3}{3 \times 81^4} = 27$, maka nilai $x$ adalah ...
A. $1$
B. $2$
C. $3$
D. $4$
Untuk menyelesaikan soal ini perlu kita ubah bentuk soal ke dalam bentuk perpangkatan dengan bilangan
pokok $3$ seperti berikut ini
$\frac{9^x \times 3^7 \times 27^3}{3 \times 81^4} = 27$
$\frac{(3^2)^x \times 3^7 \times (3^3)^3}{3 \times (3^4)^4} = 3^3$
$\frac{3^{2x} \times 3^7 \times 3^9}{3 \times 3^{16}} = 3^3$
Ingat !! untuk bilangan pokok yang sama sifat perpangkatan untuk perkalian maka pangkat dijumlahkan
apabila pembagian maka pangkat dikurangkan
$3^7 \times 3^9 = 3^{(7+9)} = 3^{16}$
$\frac{3^{2x} \times 3^{16}}{3 \times 3^{16}} = 3^3$
$\frac{3^{2x}}{3} = 3^3$
Perhatikan !! $\frac{3^{2x}}{3}$ adalah bentuk pembagian dengan bilangan pokok yang sama maka
bisa kita ubah menjadi seperti berikut
$\frac{3^{2x}}{3} = 3^{(2x-1)}$
Sehingga kita dapatkan bentuk paling sederhananya menjadi
$3^{(2x-1)} = 3^3$
Karena bilangan pokoknya sudah sama yaitu $3$, maka tinggal samakan pangkatnya seperti berikut
$2x-1 = 3$
$2x = 3+1$
$2x = 4$
$x = \frac{4}{2} = 2$
Jadi jawaban yang tepat B
Soal No 3
Hasil dari $\frac{5 \times 7^4}{7^3} - 21$ adalah ...
A. $8$
B. $10$
C. $12$
D. $14$
Perhatikan !! bentuk perpangkatan dengan bilangan pokok $7$ terjadi pembagian, sehingga bisa kita
kurangkan pangkatnya
$\frac{7^4}{7^3} = 7^{(4-3)} = 7$, maka bentuk soal menjadi sederhana
$(5 \times 7) - 21 = 35 - 21 = 14$
Jadi jawaban yang tepat D
Soal No 4
Hasil perpangkatan $6.25 \times 10^2 - 0.5 \times 10^3$ yang ditulis dalam notasi ilmiah adalah ...
A. $0.125 \times 10^2$
B. $1.25 \times 10^2$
C. $1.25 \times 10^3$
D. $1.25 \times 10^4$
Bentuk perpangkatan dengan bilangan pokok $10$ pada soal bisa kita ubah dengan menyamakan pangkat ke
pangkat terkecil. Pangkat terkecil dari soal adalah $2$ sehingga $10^3$ diubah ke bentuk pangkat $2$
$(6.25 \times 10^2) - (0.5 \times 10^3)$
$(6.25 \times 10^2) - (0.5 \times 10 \times 10^2)$
$(6.25 \times 10^2) - (5 \times 10^2)$
Sekarang kita bisa pisahkan bentuk perpangkatan menjadi seperti berikut ini
$(6.25 - 5 ) \times 10^2 = 1.25 \times 10^2$
Jadi jawaban yang tepat B
Soal No 5
Bentuk sederhana dari $\frac{64^{\frac{1}{3}} + 3}{64^{\frac{5}{6}} - 11}$ adalah ...
A. $\frac{1}{3}$
B. $\frac{1}{4}$
C. $\frac{1}{5}$
D. $\frac{1}{6}$
Untuk menyelesaikan soal ini kita ubah terlebih dahulu $64$ ke bentuk perpangkatan sebagai berikut
$64 = 2^6$, sehingga kita bisa ubah bentuk soal menjadi
$\frac{(2^6)^{\frac{1}{3}} + 3}{(2^6)^{\frac{5}{6}} - 11}$
$\frac{(2)^{\frac{6}{3}} + 3}{(2)^{\frac{6 \times 5}{6}} - 11}$
$\frac{(2)^2 + 3}{(2)^5 - 11} = \frac{4 + 3}{32 - 11} = \frac{7}{21} = \frac{1}{3}$
Jadi jawaban yang tepat A
Soal No 6
Bentuk sederhana operasi bilangan berpangkat $\sqrt{1.21 \times 10^{24}}$ adalah ...
A. $1.1 \times 10^{12}$
B. $1.1 \times 10^{13}$
C. $11 \times 10^{12}$
D. $11 \times 10^{13}$
Akar pangkat dua $\sqrt{a} = a^{\frac{1}{2}}$, sehingga
$\sqrt{1.21 \times 10^{24}} = (1.21 \times 10^{24})^{\frac{1}{2}}$
$(1.21 \times 10^{24})^{\frac{1}{2}} = [(1.1)^2 \times 10^{24}]^{\frac{1}{2}}$
$[(1.1)^2]^{\frac{1}{2}} \times [10^{24}]^{\frac{1}{2}}$
$1.1 \times 10^{12}$
Jadi jawaban yang tepat A
Soal No 7
Pada barisan berikut $8, 4, 0, -4, ...,$ beda dan suku ke-15 adalah ...
A. $b = -4, U_{15} = -48$
B. $b = -4, U_{15} = 48$
C. $b = 4, U_{15} = -48$
D. $b = 4, U_{15} = 48$
Soal di atas menyajikan bentuk barisan aritmatika. Kita tahu bahwa ciri baris aritmatika adalah mimiliki
beda, dimana beda adalah selisih dua suku yang berdampingan yaitu
$b = U_{n+1} - U_n$
Dari soal kita diberikan empat suku pertama dengan $U_1 = 8$ dan $U_2 = 4$, kita bisa hitung $b$
$b = U_2 - U_1 = 4 - 8 = -4$
Selanjutnya kita diminta mencari suku ke-15 $(U_{15})$, kita tahu rumus suku ke-n dari baris aritmatika
$U_n = U_1 + (n-1)b$
$U_{15} = 8 + (15-1)(-4)$
$U_{15} = 8 + (14)(-4)$
$U_{15} = 8 - 56 = -48$
Jadi jawaban yang tepat A
Soal No 8
Suku pertama dan ketiga suatu barisan aritmatika berturut-turut adalah $5$ dan $1$. Suku keenam barisan itu adalah ...
A. $-5$
B. $-6$
C. $-7$
D. $-8$
Diketahui :
$U_1 = 5$
$U_3 = 1$
Maka kita dapat menentukan beda $b$
$U_3 = U_1 + (3-1)b$
$1 = 5 + (2)b$
$2b = 1-5 = -4$
$b = \frac{-4}{2} = -2$
Dengan begitu kita dapat menghitung suku ke-6
$U_6 = U_1 + (6-1)b$
$U_6 = 5 + [(5) \times (-2)] = 5 - 10$
$U_6 = -5$
Jadi jawaban yang tepat A
Soal No 9
Jumlah $10$ suku pertama barisan $4+10+16+22+...$ adalah ...
A. $280$
B. $290$
C. $300$
D. $310$
Jika diperhatikan, barisan pada soal di atas adalah barisan aritmatika, karena selisih suku yang berdampingan
sama
$b = U_2 - U_1 = 10 - 4 = 6$
$b = U_3 - U_2 = 16 - 10 = 6$
$b = U_4 - U_3 = 22 - 16 = 6$
Jumlah 10 suku pertama untuk baris aritmatika bisa kita hitung dengan rumus berikut
$S_n = \frac{n}{2} \times (2U_1 + (n-1)b)$
$S_{10} = \frac{10}{2} \times (2(4) + (10-1)(6))$
$S_{10} = 5 \times (8 + (9)(6))$
$S_{10} = 5 \times (8 + 54)$
$S_{10} = 5 \times 62 = 310$
Jadi jawaban yang tepat D
Soal No 10
Berapakah $r$ dan $U_8$ dari barisan $\frac{1}{3}, \frac{1}{6}, \frac{1}{12}, \frac{1}{24}, ...$
A. $\frac{1}{2}, \frac{1}{128}$
B. $\frac{1}{2}, \frac{1}{384}$
C. $2, \frac{1}{64}$
D. $2, \frac{1}{128}$
Barisan pada soal tersebut merupakan bentuk barisan geometri, dimana ciri-cirinya memiliki rasio $r$
yang dirumuskan sebagai berikut
$r = \frac{U_n}{U_{n-1}}$
Kita ambil $U_1$ dan $U_2$
$U_1 = \frac{1}{3}$
$U_2 = \frac{1}{6}$
Maka rasio $r$ adalah
$r = \frac{U_2}{U_1} = \frac{\frac{1}{6}}{\frac{1}{3}}$
$r = \frac{1 \times 3}{1 \times 6} = \frac{1}{2}$
Untuk mencari suku ke-8 maka kita gunakan rumus $U_n$ untuk baris geometri
$U_n = U_1 \times r^{n-1}$
$U_8 = \frac{1}{3} \times (\frac{1}{2})^{8-1}$
$U_8 = \frac{1}{3} \times (\frac{1}{2})^7$
$U_8 = \frac{1}{3} \times (\frac{1}{128})$
$U_8 = \frac{1}{384}$
Jadi jawaban yang tepat B
Soal No 11
Jumlah $8$ suku pertama barisan $\frac{1}{2} + 1 + 2 + 4 + ...$ adalah ...
A. $16$
B. $32$
C. $64$
D. $\frac{255}{2}$
Jika diperhatikan, barisan tersebut adalah barisan geometri karena rasio $r$ sama
$r = \frac{U_n}{U_{n-1}}$
$r = \frac{U_2}{U_1} = \frac{1}{\frac{1}{2}} = 2$
$r = \frac{U_3}{U_2} = \frac{2}{1} = 2$
$r = \frac{U_4}{U_3} = \frac{4}{2} = 2$
Dengan begitu kita bisa menghitung jumlah $8$ suku pertama baris geometri menggunakan rumus berikut
$S_n = \frac{U_1 \times (r^n - 1)}{r-1}$
$S_8 = \frac{\frac{1}{2} \times (2^8 - 1)}{2-1}$
$S_8 = \frac{\frac{1}{2} \times (256 - 1)}{1}$
$S_8 = \frac{1}{2} \times (255) = \frac{255}{2}$
Jadi jawaban yang tepat D
Soal No 12
Budi membuka rekening di sebuah bank. Pada bulan pertama, ia menyetor uang sebesar $Rp100.000,$-. Jumlah setoran tiap
bulannya ia naikkan sebesar $Rp20.000,$- dari bulan sebelumnya. Jumlah uang Budi di bank setelah 1 tahun adalah ...
A. $Rp2.440.000,$-
B. $Rp2.480.000,$-
C. $Rp2.500.000,$-
D. $Rp2.520.000,$-
$U_1 = Rp100.000,$-
Diketahui dari informasi soal terjadi barisan aritmatika, hal ini bisa kita tebak karena setoran tiap
bulan dikatakan naik sebesar $Rp20.000,$- dari bulan sebelumnya. Artinya bulan ke-2 Budi menyetor uang
sebanyak $Rp120.000,$-, bulan ke-3 $Rp140.000,$- dst.
Sehingga dapat kita ketahui bahwa $b = Rp20.000,$-
Selanjutnya ditanyakan jumlah keseluruhan uang di bank setelah 1 tahun. Kita tahu 1 tahun terdiri atas
12 bulan, artinya kita perlu menjumlahkan uang yang disetor Budi dari bulan ke-1 sampai bulan ke-12.
Karena sudah memenuhi kriteria baris aritmatika, kita tidak perlu mencari tahu jumlah uang yang disetor
tiap bulan. Cukup gunakan rumus deret aritmatika berikut
$S_n = \frac{n}{2} \times [2U_1 + (n-1)b]$
$S_{12} = \frac{12}{2} [(2)(100.000) + (12-1)(b)]$
$S_{12} = 6 \times [200.000 + (11)(20.000)]$
$S_{12} = 6 \times (200.000 + 220.000)$
$S_{12} = 6 \times (420.000)$
$S_{12} = Rp2.520.000,$-
Jadi jawaban yang tepat D
Soal No 13
Diketahui $\triangle ABC$ dan $\triangle PQR$ kongruen, jika $\angle CAB = 75^{\circ}$, $\angle ACB = 55^{\circ}$,
$\angle PQR = 50^{\circ}$, dan $AB = PQ$, maka $\angle QPR$ adalah ...
A. $75^{\circ}$
B. $55^{\circ}$
C. $50^{\circ}$
D. $35^{\circ}$
Untuk menjawab soal ini perlu kita pahami arti kongruen terlebih dahulu. Kongruen artinya sama
dan sebangun, atau bisa kita sebut sama persis (identik).
Sehingga panjang sisi yang bersesuaian sama, dan sudut yang bersesuaian juga sama besar.
Dalam soal ini bangun datar yang dimaksudkan adalah segitiga yaitu $\triangle ABC$ dan $\triangle PQR$
kongruen.
Lebih mudah kita analisis dengan menggambarkan kedua segitiga tersebut, lihat gambar berikut

$\angle CAB = 75^{\circ}$
$\angle ACB = 55^{\circ}$
$\angle PQR = 50^{\circ}$
$AB = PQ$
Maka jelas bahwa $\angle QPR$ memiliki sudut yang bersesuaian dengan $\angle CAB$. Sehingga
$\angle QPR = \angle CAB$
$\angle QPR = 75^{\circ}$
Jadi jawaban yang tepat A
Soal No 14
Perhatikan gambar berikut !
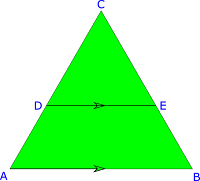
$\triangle ABC$ di atas, $DE // AB$, $DE = 8$ $cm$, $AB = 15$ $cm$, dan $CD = 6$ $cm$, panjang $AC$ adalah ...
A. $3.25$ $cm$
B. $5.35$ $cm$
C. $11.15$ $cm$
D. $11.25$ $cm$
$DE // AB$ artinya $DE$ sejajar dengan $AB$. Sehingga $\triangle ABC$ sebangun dengan $\triangle DEC$.
$DE = 8$ $cm$
$AB = 15$ $cm$
$CD = 6$ $cm$
Berdasarkan sifat kesebangunan, maka perbandingan panjang rusuk yang bersesuaian harus sama. Dalam hal
ini $AB$ bersesuaian dengan $DE$, dan $AC$ bersesuaian dengan $DC$. Sehingga $AC$ bisa kita hitung
$\frac{AC}{DC} = \frac{AB}{DE}$
$AC = DC \times \frac{AB}{DE}$
$AC = 6 \times \frac{15}{8} = 11.25$ $cm$
Jadi jawaban yang tepat D
Soal No 15
Sebidang tanah yang berukuran $160$ $m$ $\times 100$ $m$ digambar pada kertas dengan ukuran $40$ $cm$ $\times 25$ $cm$.
Skala pada gambar tersebut adalah ...
A. $1:400$
B. $1:250$
C. $1:200$
D. $1:50$
Ukuran sesungguhnya
$p_s = 160$ $m = 16.000$ $cm$
$l_s = 100$ $m = 10.000$ $cm$
Ukuran kertas
$p_k = 40$ $cm$
$l_k = 25$ $cm$
Skala adalah perbandingan ukuran di kertas dengan yang sesungguhnya
Skala Panjang
$1$ $cm$ di kertas $= \frac{p_s}{p_k}$
$1$ $cm$ di kertas $= \frac{16.000}{40}$
$1$ $cm$ di kertas $= 400$
Skala Lebar
$1$ $cm$ di kertas $= \frac{l_s}{l_k}$
$1$ $cm$ di kertas $= \frac{10.000}{25}$
$1$ $cm$ di kertas $= 400$
Artinya skala yang digunakan $1:400$
Jadi jawaban yang tepat A
Soal No 16
$\triangle PQR$ sama kaki dengan $PQ=QR=18$ $cm$, $PR=12$ $cm$. Jika $\triangle PQR$ kongruen dengan $\triangle ABC$,
maka panjang $AB$ adalah ...
A. $8$ $cm$
B. $12$ $cm$
C. $16$ $cm$
D. $18$ $cm$
Ingat !! kongruen artinya sama dan sebangun. Akan mudah dianalisis jika kita menggambarkannya,
maka perhatikan gambar berikut

$PQ=QR=18$ $cm$
$PR=12$ $cm$
Perhatikan bahwa $PQ$ bersesuaian dengan $AB$, sehingga dapat kita ketahui
$AB = PQ = 18$ $cm$
Jadi jawaban yang tepat D
Soal No 17
Diketahui $\triangle ABC$. $P$ pada $AB$ dan $Q$ pada $AC$ sedemikian sehingga $BC // PQ$. Bila panjang $AP = 9$ $cm$
dan $AB = 15$ $cm$ maka $AQ : CQ = ...$
A. $5:3$
B. $3:5$
C. $3:2$
D. $5:2$
Untuk menyelesaikan soal ini, lebih mudah kita gambarkan ilustrasinya sebagai berikut

Kita ketahui bahwa terbentuk dua buah segitiga yang sebangun yaitu $\triangle ABC$ dan $\triangle APQ$.
Dengan sisi yang bersesuaian adalah $AB$ dengan $AP$, $AC$ dengan $AQ$ dan $BC$ dengan $PQ$
$AP = 9$ $cm$
$AB = 15$ $cm$
Maka dengan sifat kesebangunan kita bisa ketahui $AQ : CQ$
$AC = AQ + CQ$
$\frac{AP}{AB} = \frac{AQ}{AC}$
$\frac{9}{15} = \frac{AQ}{AQ + CQ}$
$9(AQ + CQ) = 15AQ$
$9AQ + 9CQ = 15AQ$
$9CQ = 15AQ - 9AQ$
$9CQ = 6AQ$
$\frac{AQ}{CQ} = \frac{9}{6} = \frac{3}{2}$
Maka $AQ : CQ = 3 : 2$
Jadi jawaban yang tepat C
Soal No 18
Sebuah perahu motor penangkap ikan mempunyai panjang $30$ $m$ dan tinggi tiangnya $5$ $m$. Jika pada gambar panjangnya
$15$ $cm$, maka tinggi tiang pada gambar adalah ...
A. $15$ $cm$
B. $10$ $cm$
C. $5$ $cm$
D. $2.5$ $cm$
Ukuran Asli
$p_a = 30$ $m$
$t_a = 5$ $m$
Ukuran Gambar
$p_g = 15$ $cm$
maka tinggi pada gambar dapat dengan mudah kita hitung hanya dengan melakukan perbandingan, karena
kasus ini adalah kasus kesebangunan
$\frac{t_g}{t_a} = \frac{p_g}{p_a}$
$t_g = t_a \times \frac{p_g}{p_a}$
$t_g = 5 \times \frac{15}{30}$
$t_g = 2.5$ $cm$
Jadi jawaban yang tepat D
Soal No 19
Sebuah tabung dengan alas berjari-jari $8$ $cm$ dan tinggi $60$ $cm$ diisi air setinggi $20$ $cm$, kemudian ke dalam
tabung dimasukkan sebuah bola besi berjari-jari $7$ $cm$. Tinggi air dalam tabung sekarang adalah ...
A. $28.25$ $cm$
B. $27.15$ $cm$
C. $25.30$ $cm$
D. $20.70$ $cm$
Pertama, kita harus menghitung volume air mula-mula dalam tabung
$r_t = 8$ $cm$
$t_a = 20$ $cm$
$V_a = \pi r_t^2 t_a$
$V_a = \pi \times 8^2 \times 20$
$V_a = 1280\pi$ $cm^3$
Selanjutnya kita perlu menghitung volume bola besi
$r_b = 7$ $cm$
$V_b = \frac{4}{3} \pi r_b^3$
$V_b = \frac{4}{3} \pi \times 7^3$
$V_b = \frac{4}{3} \pi \times 343$
$V_b = \frac{1.372}{3} \pi$ $cm^3$
Karena bola besi dimasukkan ke tabung berisi air, maka air akan naik karena ada tambahan volume dari
bola. Secara matematika dituliskan sebagai berikut
$V_f = V_a + V_b$
$V_f = 1280\pi + \frac{1.372\pi}{3}$
$V_f = \frac{3.840\pi + 1.372\pi}{3}$
$V_f = \frac{5.212\pi}{3}$
Karena dalam tabung yang sama, hanya berubah ketinggian air, jadi untuk mengetahui tinggi air sekarang
bisa dicari dengan rumus volume tabung $V_f$
$V_f = \pi r_t^2 t_f$
$\frac{5.212\pi}{3} = \pi \times 8^2 \times t_f$
$\frac{5.212}{3} = 64 t_f$
$t_f = \frac{5.212}{3 \times 64} = 27.15$ $cm$
Jadi jawaban yang tepat B
Soal No 20
Perhatikan gambar berikut !

Kerucut berada di dalam tabung dan keduanya berimpit. Tinggi tabung sama dengan tinggi kerucut. Volume tabung di luar
kerucut adalah ...
A. $27.720$ $cm^3$
B. $27.216$ $cm^3$
C. $18.480$ $cm^3$
D. $4.620$ $cm^3$
$D_t = D_k = 21$ $cm$
$r_t = r_k = \frac{21}{2}$ $cm$
$t_t = t_k = 20$ $cm$
Volume tabung di luar kerucut artinya volume tabung dikurangi volume kerucut. Sehingga mudah kita hitung
$V_t = \pi r_t^2 t_t$
$V_t = \pi \times (\frac{21}{2})^2 \times 20$
$V_t = (\frac{21}{2})^2 \times 20\pi$
Lebih mudah kita gunakan $\pi = \frac{22}{7}$
$V_t = (\frac{3^2 \times 7^2 \times 20}{4}) \frac{22}{7}$
$V_t = (3^2 \times 7 \times 5) \times 22$
$V_t = 6.930$ $cm^3$ ...(1)
$V_k = \frac{1}{3} \pi r_k^2 t_k$
$V_k = \frac{1}{3} \times (\frac{21}{2})^2 \times 20\pi$
Lebih mudah kita gunakan $\pi = \frac{22}{7}$
$V_k = \frac{1}{3} \times (\frac{21}{2})^2 \times 20 \times \frac{22}{7}$
$V_k = \frac{20}{3} \times (\frac{3^2 \times 7^2}{4}) \times \frac{22}{7}$
$V_k = 5 \times (3 \times 7) \times 22$
$V_k = 2.310$ $cm^3$ ...(2)
Untuk menghitung volume diluar kerucut kita kurangkan $V_t - V_k$
$V_{lk} = V_t - V_k$
$V_{lk} = 6.930 - 2.310$
$V_{lk} = 4.620$ $cm^3$
Jadi jawaban yang tepat D
Soal No 21
Keliling alas sebuah kerucut $94,2$ $cm$, tingginya $16$ $cm$ dan $\pi = 3,14$. Volume kerucut itu adalah ...
A. $1..507,2$ $cm^3$
B. $3.768$ $cm^3$
C. $7.536$ $cm^3$
D. $11.304$ $cm^3$
$K = 94,2$ $cm$
$t = 16$ $cm$
$\pi = 3,14$
Kita tahu bahwa alas kerucut berbentuk lingkaran, sehingga
$K = 2\pi r$
$94,2 = 2 \times 3,14 r$
$r = \frac{94,2}{6,28} = 15$ $cm$
Volume kerucut dapat kita hitung dengan rumus berikut
$V = \frac{1}{3} \pi r^2 t$
$V = \frac{1}{3} \times 3,14 \times 15^2 \times 16$
$V = 3.768$ $cm^3$
Jadi jawaban yang tepat B
Soal No 22
Perhatikan gambar berikut !

Selembar seng berbentuk $\frac{3}{5}$ lingkaran dan berdiameter $60$ $cm$ akan dibuat kerucut, tinggi kerucut yang
terjadi adalah ...
A. $20$ $cm$
B. $24$ $cm$
C. $36$ $cm$
D. $46$ $cm$
Luas selembar seng tersebut berarti $\frac{3}{5}$ luas lingkaran dengan diameter $60$ $cm$ seshingga
$L_{\frac{3}{5}} = \frac{3}{5} \pi r^2$
$L_{\frac{3}{5}} = \frac{3}{5} \pi \times 30^2$
$L_{\frac{3}{5}} = 540\pi$
Karena dijadikan kerucut, maka luas $L_{\frac{3}{5}}$ adalah luas selimut kerucut. Kita tahu rumus
luas selimut kerucut sebagai berikut
$L_s = \pi r_k s$
$r_k = $ jari-jari kerucut yang terbentuk
$s = $ garis kemiringan, dalam hal ini berupa jari-jari lingkaran awal yaitu $30$ $cm$
$540\pi = \pi \times r_k \times 30$
$540 = 30r_k$
$r_k = \frac{540}{30} = 18$ $cm$
Setelah mendapatkan jari-jari kerucut, maka tinggi kerucut bisa kita hitung dengan rumus pytagoras
$t = \sqrt{s^2 - r_k^2}$
$t = \sqrt{30^2 - 18^2}$
$t = \sqrt{900 - 324}$
$t = \sqrt{576} = 24$ $cm$
Jadi jawaban yang tepat B
Soal No 23
Volume bola terbesar yang dapat dimasukkan ke dalam kubus dengan panjang rusuk $21$ $cm$ adalah ...
A. $29.106$ $cm^3$
B. $19.404$ $cm^3$
C. $9.702$ $cm^3$
D. $4.851$ $cm^3$
Karena panjang rusuk kubus $21$ $cm$, artinya bola yang bisa dimasukkan ke dalam kubus maksimal
berdiameter $21$ $cm$. Sehingga volume bola dapat kita hitung
$V_b = \frac{4}{3} \pi r^3$
$r = \frac{21}{2}$
kita gunakan $\pi = \frac{22}{7}$
$V_b = \frac{4}{3} \times \frac{22}{7} \times (\frac{21}{2})^3$
$V_b = \frac{4 \times 22 \times 7^3 \times 3^3}{3 \times 7 \times 2^3}$
$V_b = 4.851$ $cm^3$
Jadi jawaban yang tepat D
Soal No 24
Luas sebuah bola adalah $1.256$ $cm^2$. Volume bola tersebut dengan $\pi = 3,14$ adalah ... $cm^3$
A. $12.560$
B. $4.186,67$
C. $3.140$
D. $1.046,67$
Karena diketahui luas permukaan bola, maka kita tahu rumusnya
$L_p = 4\pi r^2$
$1.256 = 4\pi r^2$
$\pi r^2 = \frac{1.256}{4} = 314$
$r^2 = \frac{314}{\pi} = \frac{314}{3,14}$
$r^2 = 100$
$r = \sqrt{100} = 10$ $cm$
Setelah mengetahui jari-jari, kita bisa hitung volume
$V_b = \frac{4}{3} \pi r^3$
$V_b = \frac{4}{3} \times 3,14 \times 10^3$
$V_b = \frac{4}{3} \times 3.140$
$V_b = 4.186,67$ $cm^3$
Jadi jawaban yang tepat B
Soal No 25
Sebuah data hasil ulangan Matematika kelas IX B menunjukkan, 6 siswa mendapat nilai 90, 8 siswa mendapat nilai 85, 10
siswa mendapat nilai 80, 6 siswa mendapat nilai 75 dan 2 siswa mendapat nilai 70. Rata-rata nilai ulangan matematika
kelas tersebut adalah ...
A. $81,36$
B. $81,56$
C. $81,63$
D. $81,65$
$\bar x = \frac{\Sigma x_i n_i}{\Sigma n_i}$
$\bar x = \frac{(90 \times 6)+(85 \times 8)+(80 \times 10)+(75 \times 6)+(70 \times 2)}
{6+8+10+6+2}$
$\bar x = \frac{(540)+(680)+(800)+(450)+(140)}{32}$
$\bar x = \frac{2.610}{32} = 81,56$
Jawaban yang tepat B
Soal No 26
Perhatikan data berikut ini !
$8,7,7,6,5,5,8,9,10,12,8,9$
Nilai median dan modus data di atas adalah ...
A. $7,5$ dan $8$
B. $8$ dan $7$
C. $8$ dan $8$
D. $8,5$ dan $8$
Median adalah data tengah yang telah disusun, akan mudah diketahui jika kita menyusun terlebih dahulu
seperti berikut ini
$5,5,6,7,7,|8,8|,8,9,9,10,12$
Data tengah berada di |8 dan 8|, maka bisa ditentukan dengan cara berikut
$Me = \frac{8+8}{2} = 8$
Modus adalah data yang paling sering muncul, dalam hal ini dapat kita lihat bahwa data $8$ muncul tiga
kali sedangkan tidak ada data lain yang muncul lebih dari tiga kali
Sehingga $Mo = 8$
Jadi jawaban yang tepat C
Soal No 27
Di bawah ini adalah data banyak anak pada tiap-tiap keluarga RT.05/RW.02 kelurahan Suka Makmur

Banyak anak dan banyak keluarga dalam lingkungan tersebut adalah ...
A. $49$ dan $22$
B. $50$ dan $22$
C. $49$ dan $23$
D. $50$ dan $23$
Satu keluarga punya 5 anak
Dua keluarga masing-masing punya 0 anak
Empat keluarga masing-masing punya 3 dan 4 anak
Lima keluarga masing-masing punya 2 anak
Enam keluarga masing-masing punya 1 anak
Jumlah keluarga :
$1+2+4+4+5+6 = 22$ keluarga
Jumlah Anak
Satu keluarga = $5$ anak
Dua keluarga = $0$ anak
Empat keluarga :
Lima keluarga = $5 \times 2 = 10$ anak
Enam keluarga = $6 \times 1 = 6$ anak
Jumlah Anak :
$5+0+12+16+10+6 = 49$
Jadi jawaban yang tepat A
Soal No 28
Diketahui data nilai ulangan akhir semester kelas IX A SMP Sukaraja di bawah ini

Jika nilai UAS siswa di kelas tersebut memiliki rata-rata $7,48$, maka nilai $n$ adalah ...
A. $1$
B. $2$
C. $3$
D. $4$
$\bar x = \frac{\Sigma x_i n_i}{\Sigma n_i}$
$7,48 = \frac{(6 \times 5)+(7 \times 7)+(8 \times 10)+(9 \times n)+(10 \times 1)}
{5+7+10+n+1}$
$7,48 = \frac{30+49+80+9n+10}{23+n}$
$7,48\times (23+n) = 169+9n$
$172,04 + 7,48n = 169+9n$
$172,04 - 169 = 9n - 7,48n$
$3,04 = 1,52n$
$n = \frac{3,04}{1,52} = 2$
Jadi jawaban yang tepat B
Soal No 29
Diagram berikut ini menunjukkan jumlah kebutuhan Pak Asep dalam satu bulan

A untuk makan
B untuk transportasi
C untuk tabungan
D untuk lain-lain
Jika penghasilan pak Asep $6$ juta rupiah, maka banyaknya uang yang digunakan untuk kebutuhan makan adalah ...
A. $Rp. 750.000,$-
B. $Rp. 1.000.000,$-
C. $Rp. 1.200.000,$-
D. $Rp. 1.250.000,$-
Untuk mengetahui kebutuhan makan, perlu kita tahu besar sudut bagian A. Kita tahu :
$\angle B = 30^\circ$
$\angle C = 90^\circ$
$\angle D = 180^\circ$
Karena sudut total lingkaran adalah $360^\circ$, maka mudah kita cari $\angle A$
$\angle A = 360^\circ - (\angle B + \angle C + \angle D)$
$\angle A = 360^\circ - (30^\circ + 90^\circ + 180^\circ)$
$\angle A = 60^\circ$
Maka untuk menghitung kebutuhan makan dapat kita cari menggunakan perbandingan
Makan $= \frac{60^\circ}{360^\circ} \times 6$
Makan $= \frac{1}{6} \times 6$
Makan $= 1$ Juta
Kebutuhan untuk makan adalah $Rp. 1.000.000,$-
Jadi jawaban yang tepat B
Soal No 30
Nilai rata-rata dari $48$ orang siswa adalah $6,00$. Setelah ditambahkan dengan nilai dua orang, ternyata rata-ratanya
menjadi $6,06$. Nilai rata-rata dari dua orang terakhir adalah ...
A. $6,5$
B. $7,0$
C. $7,5$
D. $8,0$
$n_a = 48$
$\bar{x}_a = 6,00$
$n_2 = 2$
$n_f = n_a + n_2$
$n_f = 48 + 2 = 50$
$\bar{x}_f = 6,06$
$\bar{x}_f = \frac{(\bar{x}_a \times n_a)+(\bar{x}_2 \times n_2)}{n_f}$
$6,06 = \frac{(6,00 \times 48)+(\bar{x}_2 \times 2)}{50}$
$50 \times 6,06 = 288 + 2 \bar{x}_2$
$303 = 288 + 2 \bar{x}_2$
$303 - 288 = 2 \bar{x}_2$
$303 - 288 = 2 \bar{x}_2$
$15 = 2 \bar{x}_2$
$\bar{x}_2 = \frac{15}{2} = 7,5$
Jadi jawaban yang tepat C
Soal Esai
Soal No 31
Sederhanakan operasi perpangkatan berikut :
Bagian a
$m^2 \times (5m^2)^3$
$m^2 \times (5^3 \times m^6)$
$125 m^8$
Bagian b
$\frac{6^6 \times 6^2}{\sqrt{36}}$
$\frac{6^8}{6} = 6^7$
Bagian c
$49^{\frac{3}{2}}$
$(7^2)^{\frac{3}{2}} = 7^3$
Soal No 32
Seutas tali dipotong menjadi $7$ bagian yang membentuk deret geometri. Apabila potongan terpendek adalah $3$ $m$ dan
potongan terpanjang adalah $192$ $m$. Tentukan panjang tali mula-mula !
Tal dipotong menjadi $7$ bagian artinya terdapat $7$ suku geometri. Karena diketahui yang terpanjang dan
yang terpendek, maka dapat kita ketahui sebagai berikut
$U_1 =$ terpendek $= 3$ $m$
$U_7 =$ terpanjang $= 192$ $m$
Rumus barisan dan deret geometri untuk suku ke-$n$ adalah sebagai berikut
$U_n = U_1 \times r^{n-1}$
$U_7 = U_1 \times r^{7-1}$
$192 = 3 \times r^6$
$r^6 = {192}{3} = 64$
$r^6 = 2^6$
$r^6 = 2^6$
$r = 2$
Panjang tali mula-mula berarti jumlah $7$ baris geometri
$S_n = \frac{U_1 \times (r^n - 1)}{r - 1}$
$S_7 = \frac{3 \times (2^7 - 1)}{2 - 1}$
$S_7 = \frac{3 \times (128 - 1)}{1}$
$S_7 = 3 \times (127) = 381$ $m$
Jadi panjang mula-mula tali adalah $381$ $meter$
Soal No 33
Diketahui dua persegi panjang masing-masing berukuran $20$ $cm$ $\times 15$ $cm$ dan $28$ $cm$ $\times 21$ $cm$. Apakah
kedua persegi panjang tersebut sebangun ? Jelaskan !
Untuk mencari tahu suatu bangun datar sebangun atau tidak mudah kita lakukan dengan melakukan perbandingan
sisi-sisi yang bersesuaian. Dalam soal ini diketahui
$p_1 = 20$ $cm$
$l_1 = 15$ $cm$
$p_2 = 28$ $cm$
$l_2 = 21$ $cm$
Mari kita jadikan salah satu bangun datar sebagai bangun datar acuan. Disini yang saya jadikan acuan
adalah $p_1$, $l_1$ dan $l_2$. Selanjutnya kita hitung $p_2$ yang seharusnya, jika sesuai dengan data
dari soal, maka bangun tersebut sebangun
$\frac{p_2}{p_1} = \frac{l_2}{l_1}$
$\frac{p_2}{20} = \frac{21}{15} = \frac{7}{5}$
$p_2 = 20 \times \frac{7}{5} = 28$ $cm$
Ternyata sudah sesuai, artinya bangun datar persegi panjang tersebut sebangun.
Soal No 34
Perhatikan gambar berikut ini !

Tentukan luas permukaan bangun ruang tersebut !
$D_t = D_k = 10$ $cm$
$r_t = r_k = 5$ $cm$
$t_t = 8$ $cm$
$t_k = 12$ $cm$
Ditanyakan luas permukaan terdiri atas luas permukaan alas tabung, selimut tabung, selimut kerucut.
L{total} = L_{alas} + L_{st} + L_{sk}$
Luas Alas Tabung
$L_{alas} = \pi r_t^2$
$L_{alas} = 3,14 \times 5^2$
$L_{alas} = 3,14 \times 25 = 78,5$ $cm^2$
Luas Selimut Tabung
$L_{st} = \pi D_t t_t$
$L_{st} = 3,14 \times 10 \times 8$
$L_{st} = 251,2$ $cm^2$
Luas Selimut Kerucut
$L_{sk} = \pi D_k s$
$s$ adalah kemiringan kerucut, dapat dicari dengan pytagoras
$s = \sqrt{r_k^2 + t_k^2}$
$s = \sqrt{5^2 + 12^2}$
$s = \sqrt{25 + 144}$
$s = \sqrt{169} = 13$ $cm$
$L_{sk} = 3,14 \times 10 \times 13$
$L_{sk} = 408,2$ $cm^2$
$L_{total} = L_{alas} + L_{st} + L_{sk}$
$L_{total} = 78,5 + 251,2 + 408,2$
$L_{total} = 737,9$ $cm^2$
Jadi luas permukaan bangun ruang tersebut adalah $737,9$ $cm^2$
Soal No 35
Apabila perbandingan jumlah perempuan dan laki-laki dalam satu kelas adalah $3:2$ dan jumlah perempuan ada $15$.
Tentukan rata-rata berat badan laki-laki jika total berat badan siswa laki-laki adalah $425$ !
Disini kita diberi tahu perbandingan perempuan dan laki-laki dan jumlah perempuan
$\frac{P}{L} = \frac{3}{2}$
$P = 15$
Berat total laki-laki $BL = 425$
Kita perlu tahu dulu jumlah laki-laki dengan perbandingan
$\frac{15}{L} = \frac{3}{2}$
$\frac{15 \times 2}{3} = L$
$L = 10$
Karena kita telah diberitahu berat total siswa laki-laki, maka kita bisa mengetahui rata-rata berat
laki-laki
$\bar{BL} = \frac{BL}{L} = \frac{425}{10}$
$\bar{BL} = 42,4$ $kg$
Penutup
Demikian soal matematika PAS SMP/MTs kelas 9 beserta kunci jawaban yang bisa saya tuliskan pada kesempatan ini. Semoga
dapat membantu sobat untuk latihan soal matematika sebagai persiapan Penilaian Akhir Semester agar lebih memahami bentuk
soal yang akan diujiankan.
Semakin banyak berlatih mengerjakan soal, maka ketajaman dalam mengerjakan soal matematika akan akan semakin baik.
Sehingga sobat akan bisa mengerjakan PAS dengan lancar dan mudah pada waktunya.
Semoga bermanfaat dan terima kasih atas kunjungannya.









